Plotting using `predict`

September 12, 2016

One of my favorite functions in R is predict, and so in response to this recent question on SlackRs#plots (“Anyone know how to plot an interaction at a moderators mean, +1SD, and -1SD?”) I thought I’d write up a quick demo of it’s usefulness.

Let’s assume a simple interaction effect between two continuous variables:

$y = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + \beta_{3}x_{1}x_{2}+\epsilon$

set.seed(92299)
N <- 500
b0 <- 0
b1 <- .3
b2 <- .5
b3 <- -.2

aDF <- within(data.frame(x1=rnorm(N)), 
     {
	     x2 <- rnorm(N)
	     x1x2 <- x1*x2
	     y <- b0+b1*x1+b2*x2+b3*x1x2+rnorm(N,0,1)
     })

head(aDF)

##           x1           y        x1x2          x2
## 1 -0.4732279  0.79910376 -0.55652246  1.17601350
## 2  0.2699430  0.18102388 -0.31458272 -1.16536700
## 3 -1.1218179  1.15182465 -1.24691895  1.11151635
## 4  0.1047639  1.58974408  0.06749747  0.64428201
## 5 -0.7177402 -1.80769438 -0.14404438  0.20069152
## 6  1.5776371  0.07835544 -0.10464178 -0.06632817

Now that we’ve generated data, we can fit a model:

aMod <- lm(y~1+x1*x2, aDF)
summary(aMod)

## 
## Call:
## lm(formula = y ~ 1 + x1 * x2, data = aDF)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.2827 -0.6737  0.0105  0.6840  3.1072 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.05362    0.04495  -1.193    0.233    
## x1           0.30942    0.04223   7.327 9.58e-13 ***
## x2           0.51358    0.04289  11.975  < 2e-16 ***
## x1:x2       -0.16785    0.03765  -4.458 1.02e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.001 on 496 degrees of freedom
## Multiple R-squared:  0.3147,	Adjusted R-squared:  0.3106 
## F-statistic: 75.93 on 3 and 496 DF,  p-value: < 2.2e-16

How do we plot the relationship between y and x1 at different levels of x2? We can use predict to get the expected y for every x1 at the mean and +/-1 SD of x2 by creating a new data frame with those values.

minx1 <- min(aDF$x1)
maxx1 <- max(aDF$x1)
steps <- 100 #we want to get y values for 100 values in the real range of x1 
x1_values <- seq(minx1, 
		 maxx1, 
		 length.out=steps)
#We'll use `rep` to repeat these values for every value of x2 we want below...
x2.sd <- sd(aDF$x2)
x2.mean <- mean(aDF$x2)

newData <- data.frame(x1=rep(x1_values, 3), #for each val of x2
		      x2=rep(c(x2.mean-x2.sd,
			       x2.mean,
			       x2.mean+x2.sd), 
			     each=steps),
		      x2_level=rep(c('-1 SD',
				     'Mean',
				     '+1 SD'),
				   each=steps)) #each val of x2 for all x1
head(newData)

##          x1        x2 x2_level
## 1 -2.992855 -1.065048    -1 SD
## 2 -2.931769 -1.065048    -1 SD
## 3 -2.870684 -1.065048    -1 SD
## 4 -2.809598 -1.065048    -1 SD
## 5 -2.748513 -1.065048    -1 SD
## 6 -2.687427 -1.065048    -1 SD

Now use predict to get y values.

newData$y <- predict(aMod,newdata = newData) 
head(newData)

##          x1        x2 x2_level         y
## 1 -2.992855 -1.065048    -1 SD -2.061668
## 2 -2.931769 -1.065048    -1 SD -2.031847
## 3 -2.870684 -1.065048    -1 SD -2.002026
## 4 -2.809598 -1.065048    -1 SD -1.972205
## 5 -2.748513 -1.065048    -1 SD -1.942384
## 6 -2.687427 -1.065048    -1 SD -1.912564

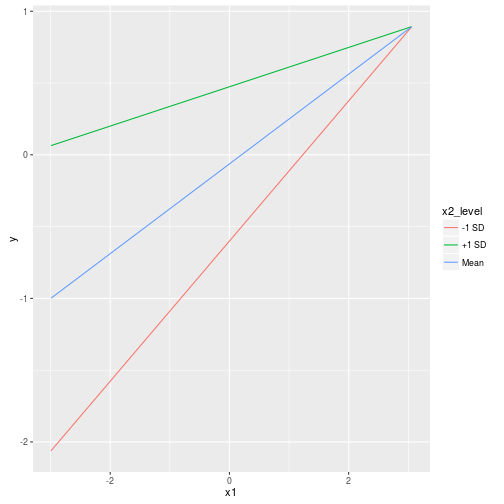
Let’s plot it using ggplot2.

library(ggplot2)
ggplot(newData, aes(x=x1, y=y, group=x2_level, color=x2_level))+
	geom_line()

center